2.2.1.4.1. Main point¶
The question:
>>> x = np.array([[1, 2, 3],
... [4, 5, 6],
... [7, 8, 9]], dtype=np.int8)
>>> str(x.data)
'\x01\x02\x03\x04\x05\x06\x07\x08\t'
At which byte in ``x.data`` does the item ``x[1, 2]`` begin?
The answer (in Numpy)
- strides: the number of bytes to jump to find the next element
- 1 stride per dimension
>>> x.strides
(3, 1)
>>> byte_offset = 3*1 + 1*2 # to find x[1, 2]
>>> x.flat[byte_offset]
6
>>> x[1, 2]
6
- simple, **flexible**
2.2.1.4.1.1. C and Fortran order¶
>>> x = np.array([[1, 2, 3],
... [4, 5, 6]], dtype=np.int16, order='C')
>>> x.strides
(6, 2)
>>> str(x.data)
'\x01\x00\x02\x00\x03\x00\x04\x00\x05\x00\x06\x00'
- Need to jump 6 bytes to find the next row
- Need to jump 2 bytes to find the next column
>>> y = np.array(x, order='F')
>>> y.strides
(2, 4)
>>> str(y.data)
'\x01\x00\x04\x00\x02\x00\x05\x00\x03\x00\x06\x00'
- Need to jump 2 bytes to find the next row
- Need to jump 4 bytes to find the next column
Similarly to higher dimensions:
- C: last dimensions vary fastest (= smaller strides)
- F: first dimensions vary fastest
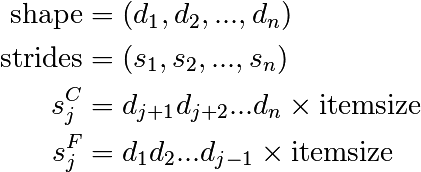
Note
Now we can understand the behavior of .view():
>>> y = np.array([[1, 3], [2, 4]], dtype=np.uint8).transpose()
>>> x = y.copy()
Transposition does not affect the memory layout of the data, only strides
>>> x.strides
(2, 1)
>>> y.strides
(1, 2)
>>> str(x.data)
'\x01\x02\x03\x04'
>>> str(y.data)
'\x01\x03\x02\x04'
- the results are different when interpreted as 2 of int16
- .copy() creates new arrays in the C order (by default)
2.2.1.4.1.2. Slicing with integers¶
- Everything can be represented by changing only shape, strides, and possibly adjusting the data pointer!
- Never makes copies of the data
>>> x = np.array([1, 2, 3, 4, 5, 6], dtype=np.int32)
>>> y = x[::-1]
>>> y
array([6, 5, 4, 3, 2, 1], dtype=int32)
>>> y.strides
(-4,)
>>> y = x[2:]
>>> y.__array_interface__['data'][0] - x.__array_interface__['data'][0]
8
>>> x = np.zeros((10, 10, 10), dtype=np.float)
>>> x.strides
(800, 80, 8)
>>> x[::2,::3,::4].strides
(1600, 240, 32)
Similarly, transposes never make copies (it just swaps strides):
>>> x = np.zeros((10, 10, 10), dtype=np.float) >>> x.strides (800, 80, 8) >>> x.T.strides (8, 80, 800)
But: not all reshaping operations can be represented by playing with strides:
>>> a = np.arange(6, dtype=np.int8).reshape(3, 2)
>>> b = a.T
>>> b.strides
(1, 2)
So far, so good. However:
>>> str(a.data)
'\x00\x01\x02\x03\x04\x05'
>>> b
array([[0, 2, 4],
[1, 3, 5]], dtype=int8)
>>> c = b.reshape(3*2)
>>> c
array([0, 2, 4, 1, 3, 5], dtype=int8)
Here, there is no way to represent the array c given one stride and the block of memory for a. Therefore, the reshape operation needs to make a copy here.

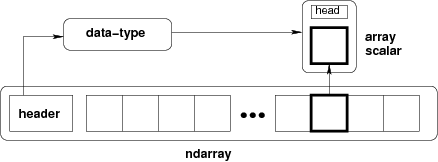
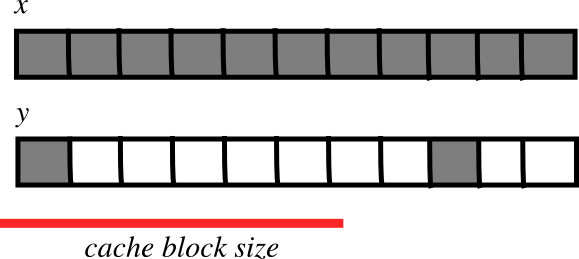
 fewer transfers needed
fewer transfers needed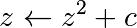
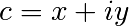 is a complex number. This iteration is
repeated – if
is a complex number. This iteration is
repeated – if 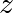 stays finite no matter how long the iteration
runs,
stays finite no matter how long the iteration
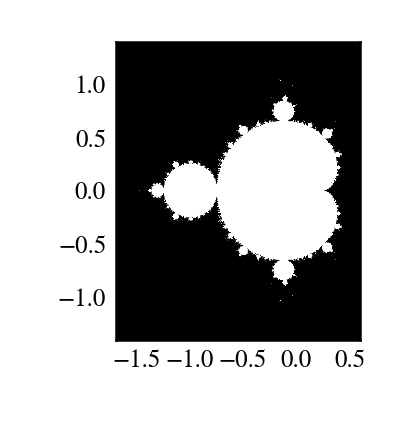
runs, 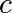 belongs to the Mandelbrot set.
belongs to the Mandelbrot set.