The exercise goal is to predict the maximum wind speed occurring every 50 years even if no measure exists for such a period. The available data are only measured over 21 years at the Sprogø meteorological station located in Denmark. First, the statistical steps will be given and then illustrated with functions from the scipy.interpolate module. At the end the interested readers are invited to compute results from raw data and in a slightly different approach.
The annual maxima are supposed to fit a normal probability density function. However such function is not going to be estimated because it gives a probability from a wind speed maxima. Finding the maximum wind speed occurring every 50 years requires the opposite approach, the result needs to be found from a defined probability. That is the quantile function role and the exercise goal will be to find it. In the current model, it is supposed that the maximum wind speed occurring every 50 years is defined as the upper 2% quantile.
By definition, the quantile function is the inverse of the cumulative distribution function. The latter describes the probability distribution of an annual maxima. In the exercise, the cumulative probability p_i for a given year i is defined as p_i = i/(N+1) with N = 21, the number of measured years. Thus it will be possible to calculate the cumulative probability of every measured wind speed maxima. From those experimental points, the scipy.interpolate module will be very useful for fitting the quantile function. Finally the 50 years maxima is going to be evaluated from the cumulative probability of the 2% quantile.
The annual wind speeds maxima have already been computed and saved in the numpy format in the file examples/max-speeds.npy, thus they will be loaded by using numpy:
>>> import numpy as np
>>> max_speeds = np.load('intro/summary-exercises/examples/max-speeds.npy')
>>> years_nb = max_speeds.shape[0]
Following the cumulative probability definition p_i from the previous section, the corresponding values will be:
>>> cprob = (np.arange(years_nb, dtype=np.float32) + 1)/(years_nb + 1)
and they are assumed to fit the given wind speeds:
>>> sorted_max_speeds = np.sort(max_speeds)
In this section the quantile function will be estimated by using the UnivariateSpline class which can represent a spline from points. The default behavior is to build a spline of degree 3 and points can have different weights according to their reliability. Variants are InterpolatedUnivariateSpline and LSQUnivariateSpline on which errors checking is going to change. In case a 2D spline is wanted, the BivariateSpline class family is provided. All those classes for 1D and 2D splines use the FITPACK Fortran subroutines, that’s why a lower library access is available through the splrep and splev functions for respectively representing and evaluating a spline. Moreover interpolation functions without the use of FITPACK parameters are also provided for simpler use (see interp1d, interp2d, barycentric_interpolate and so on).
For the Sprogø maxima wind speeds, the UnivariateSpline will be used because a spline of degree 3 seems to correctly fit the data:
>>> from scipy.interpolate import UnivariateSpline
>>> quantile_func = UnivariateSpline(cprob, sorted_max_speeds)
The quantile function is now going to be evaluated from the full range of probabilities:
>>> nprob = np.linspace(0, 1, 1e2)
>>> fitted_max_speeds = quantile_func(nprob)
In the current model, the maximum wind speed occurring every 50 years is defined as the upper 2% quantile. As a result, the cumulative probability value will be:
>>> fifty_prob = 1. - 0.02
So the storm wind speed occurring every 50 years can be guessed by:
>>> fifty_wind = quantile_func(fifty_prob)
>>> fifty_wind
array(32.97989825...)
The results are now gathered on a Matplotlib figure:
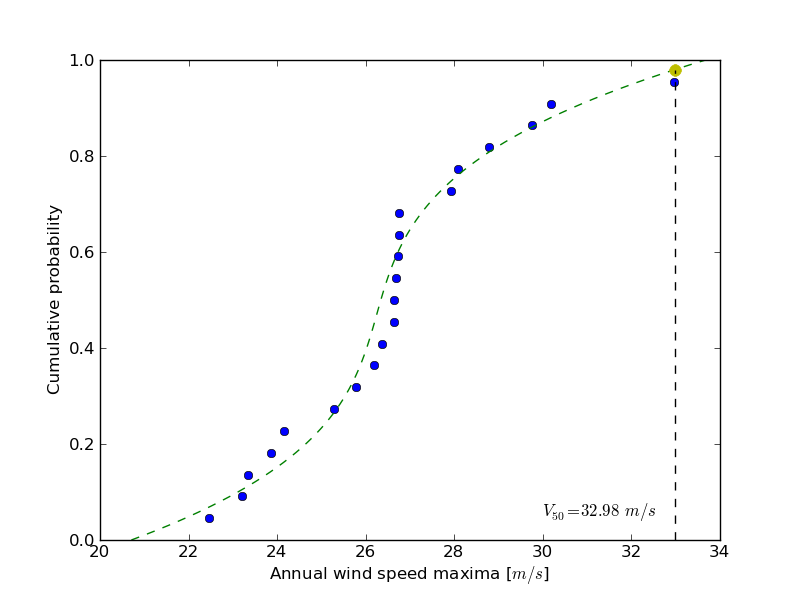
Solution: Python source file
The interested readers are now invited to make an exercise by using the wind speeds measured over 21 years. The measurement period is around 90 minutes (the original period was around 10 minutes but the file size has been reduced for making the exercise setup easier). The data are stored in numpy format inside the file examples/sprog-windspeeds.npy. Do not look at the source code for the plots until you have completed the exercise.
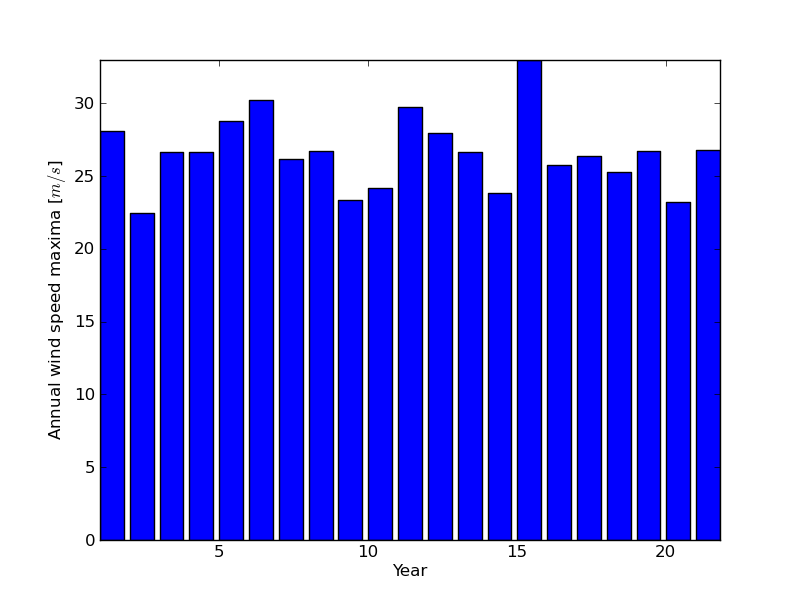
Solution: Python source file
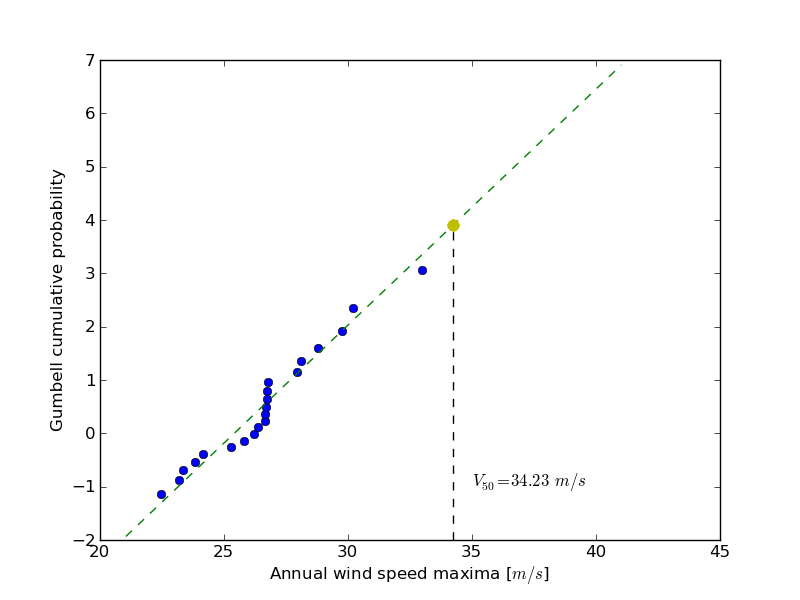
Solution: Python source file